Les paramétrisations
Au choix d’un maillage pour résoudre les équations, correspond le choix d’une échelle spatiale. Tous les processus se situant à une échelle inférieure à celle du maillage ne peuvent pas être représentés de manière explicite. Une maille de modèle climatique est un carré d’environ 200 km de côté. Il suffit de lever le nez pour voir qu’un nuage est souvent bien plus petit que cela. De même, la turbulence océanique ou atmosphérique sont des phénomènes d’échelles plus petites que la maille d’un modèle.
Les modèles utilisent alors des lois simplifiées, empiriques, que l’on appelle des paramétrisations. Ces lois reposent sur un principe très fort, et bien vérifié empiriquement : l’écoulement de grande échelle détermine de manière suffisamment forte les écoulements de petite échelle, pour que sa seule connaissance permette d’estimer le rôle statistique de ces petites échelles. La représentation des nuages en est un exemple frappant de ces interactions entre échelles et des difficultés de modélisation associées : les nuages sont générés par des mouvements de l’air allant de quelques centaines de mètres à quelques kilomètres, mouvements qu’il est hors de question de représenter de manière explicite dans les modèles ; ils sont aussi le lieu d’un dégagement de chaleur latente intense, qui résulte de la condensation de l’eau, et ils perturbent le rayonnement solaire et le rayonnement infrarouge d’une manière qui dépend fortement de la taille des gouttes d’eau ou des cristaux de glace. Devant tant de complexité — et l’on pourrait donner d’autres exemples, relatifs aux glaces de mer, aux tourbillons océaniques, à la végétation ou à l’hydrologie continentale — la modélisation est donc nécessairement simplificatrice. Elle n’est pas pour autant simpliste, et la représentation des nuages dans les modèles a fait l’objet d’un travail considérable (s’appuyant sur des mesures par ballons, avions et satellites) pour l’appuyer sur une description statistique des processus de formation des gouttes d’eau, des mouvements de l’air humide, ou de la précipitation. De plus il est important de réaliser que les lois statistiques ou empiriques décrivant les nuages (ou tous les processus de petite échelle) sont bien des lois et non des ajustements locaux : elles sont appliquées à toutes les mailles du modèle global, selon une formulation inchangée de l’équateur aux pôles.
Les modèles utilisent alors des lois simplifiées, empiriques, que l’on appelle des paramétrisations. Ces lois reposent sur un principe très fort, et bien vérifié empiriquement : l’écoulement de grande échelle détermine de manière suffisamment forte les écoulements de petite échelle, pour que sa seule connaissance permette d’estimer le rôle statistique de ces petites échelles. La représentation des nuages en est un exemple frappant de ces interactions entre échelles et des difficultés de modélisation associées : les nuages sont générés par des mouvements de l’air allant de quelques centaines de mètres à quelques kilomètres, mouvements qu’il est hors de question de représenter de manière explicite dans les modèles ; ils sont aussi le lieu d’un dégagement de chaleur latente intense, qui résulte de la condensation de l’eau, et ils perturbent le rayonnement solaire et le rayonnement infrarouge d’une manière qui dépend fortement de la taille des gouttes d’eau ou des cristaux de glace. Devant tant de complexité — et l’on pourrait donner d’autres exemples, relatifs aux glaces de mer, aux tourbillons océaniques, à la végétation ou à l’hydrologie continentale — la modélisation est donc nécessairement simplificatrice. Elle n’est pas pour autant simpliste, et la représentation des nuages dans les modèles a fait l’objet d’un travail considérable (s’appuyant sur des mesures par ballons, avions et satellites) pour l’appuyer sur une description statistique des processus de formation des gouttes d’eau, des mouvements de l’air humide, ou de la précipitation. De plus il est important de réaliser que les lois statistiques ou empiriques décrivant les nuages (ou tous les processus de petite échelle) sont bien des lois et non des ajustements locaux : elles sont appliquées à toutes les mailles du modèle global, selon une formulation inchangée de l’équateur aux pôles.
Exemple de paramétrisation : le schéma de convection atmosphérique
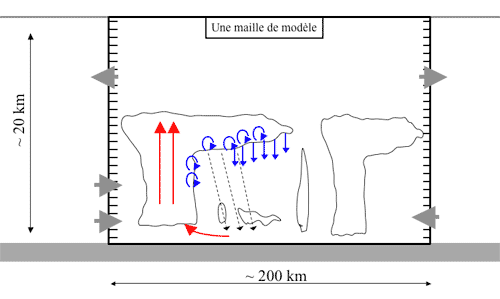
Légende
La figure représente une maille horizontale de modèle (cardre noir). La maille est divisé en niveaux verticaux. Dans et autour des nuages existent de très forts mouvements verticaux. Les flèches rouges montrent les forts mouvements ascendants dans un nuage convectif, de type cumulo-nimbus par exemple. Les flèches bleues indiquent les mouvements descendants et la turbulence active dans et autour du nuage. Ces mouvements ne sont pas explicitement représentés par le modèle. On souhaite toutefois représenter l’effet de ces vents verticaux sur les échanges d’air et d’eau entre les différentes couches de l’atmosphère. A partir des vents à grande échelle calculés par le modèle, représentés par les flèches grises, on calcule une statistique de ces échanges. Cette statistique est obtenue à partir de considérations physiques. Un fort apport d’humidité dans les basses couches favorise la formation de nuages convectifs. Une structure de l’atmosphère stable, avec un fort gradient vertical de température, est moins favorable qu’une structure plus homogène. Des campagnes de mesures et des modélisations à des échelles très fines des nuages permettent la formation de nuages et leur structure à la dynamique de grande échelle de l’atmosphère.